Какова плотность пресной воды и от чего она зависит?

Физические свойства воды при температуре от 0 до 100°С

В таблице представлены следующие физические свойства воды: плотность воды ρ, удельная энтальпия h, удельная теплоемкость C_p, теплопроводность воды λ, температуропроводность воды а, вязкость динамическая μ, вязкость кинематическая ν, коэффициент объемного теплового расширения β, коэффициент поверхностного натяжения σ, число Прандтля Pr. Физические свойства воды приведены в таблице при нормальном атмосферном давлении в интервале от 0 до 100°С.

Физические свойства воды существенно зависят от ее температуры. Наиболее сильно эта зависимость выражена у таких свойств, как удельная энтальпия и динамическая вязкость. При нагревании значение энтальпии воды значительно увеличивается, а вязкость существенно снижается. Другие физические свойства воды, например, коэффициент поверхностного натяжения, число Прандтля и плотность уменьшаются при росте ее температуры. К примеру, плотность воды при нормальных условиях (20°С) имеет значение 998,2 кг/м3, а при температуре кипения снижается до 958,4 кг/м3.

Такое свойство воды, как теплопроводность (или правильнее — коэффициент теплопроводности) при нагревании имеет тенденцию к увеличению. Теплопроводность воды при температуре кипения 100°С достигает значения 0,683 Вт/(м·град). Температуропроводность H₂O также увеличивается при росте ее температуры.

Следует отметить нелинейное поведение кривой зависимости удельной теплоемкости этой жидкости от температуры. Ее значение снижается в интервале от 0 до 40°С, затем происходит постепенный рост теплоемкости до величины 4220 Дж/(кг·град) при 100°С.

Физические свойства воды при атмосферном давлении — таблица

t, °С →	10	20	30	40	50	60	70	80	90	100
ρ, кг/м3	999,8	999,7	998,2	995,7	992,2	988	983,2	977,8	971,8	965,3	958,4
h, кДж/кг	42,04	83,91	125,7	167,5	209,3	251,1	293	335	377	419,1
Cp, Дж/(кг·град)	4217	4191	4183	4174	4174	4181	4182	4187	4195	4208	4220
λ, Вт/(м·град)	0,569	0,574	0,599	0,618	0,635	0,648	0,659	0,668	0,674	0,68	0,683
a·108, м2/с	13,2	13,7	14,3	14,9	15,3	15,7	16	16,3	16,6	16,8	16,9
μ·106, Па·с	1788	1306	1004	801,5	653,3	549,4	469,9	406,1	355,1	314,9	282,5
ν·106, м2/с	1,789	1,306	1,006	0,805	0,659	0,556	0,478	0,415	0,365	0,326	0,295
β·104, град-1	-0,63	0,7	1,82	3,21	3,87	4,49	5,11	5,7	6,32	6,95	7,52
σ·104, Н/м	756,4	741,6	726,9	712,2	696,5	676,9	662,2	643,5	625,9	607,2	588,6
Pr	13,5	9,52	7,02	5,42	4,31	3,54	2,93	2,55	2,21	1,95	1,75

Примечание: Температуропроводность в таблице дана в степени 108 , вязкость в степени 106 и т. д. для других свойств. Размерность физических свойств воды выражена в единицах СИ.

«Эврика!» Открытие закона Архимеда

Однажды царь Сиракуз Гиерон II обратился к Архимеду с просьбой установить, действительно ли его корона выполнена из чистого золота, как утверждал ювелир. Правитель подозревал, что мастер прикарманил часть драгоценного металла и частично заменил его серебром.

В те времена не существовало способов определить химический состав металлического сплава. Задача поставила учёного в тупик. Размышляя над ней, он отправился в баню и лёг в ванну, до краёв наполненную водой. Когда часть воды вылилась наружу, на Архимеда снизошло озарение. Такое, что учёный голышом выскочил на улицу и закричал «Эврика!», что по-древнегречески означает «Нашёл!».

Он предположил, что вес вытесненной воды был равен весу его тела, и оказался прав. Явившись к царю, он попросил принести золотой слиток, равный по весу короне, и опустить оба предмета в наполненные до краёв резервуары с водой. Корона вытеснила больше воды, чем слиток. При одной и той же массе объём короны оказался больше, чем объём слитка, а значит, она обладала меньшей плотностью, чем золото. Выходит, царь правильно подозревал своего ювелира.

Так был открыт принцип, который теперь мы называем законом Архимеда:

На тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объёме погружённой части тела.

Эта выталкивающая сила и называется силой Архимеда.

<<Форма демодоступа>>

Физическое определение

Согласно физическому определению, плотность — это отношение массы к объему.

То есть, эта величина показывает количество данного вещества, сосредоточенного в определенном объеме.

Если посмотреть на молекулярном уровне, плотность показывает, насколько близко друг к другу расположены молекулы того или иного материала.

Показателем, иллюстрирующим значение этого параметра, может стать соотношение веса 1 л разных жидкостей:

• вода — 1 кг;
• масло — 900 г;
• спирт — 800 г и т.д.

То есть, в одинаковом объеме воды больше, чем масла или спирта. Для обозначения плотности в формулах используется греческая буква ρ (ро).

Сама формула в общем виде выглядит следующим образом:

ρ =m/V, где

• m — масса;
• V — объем.

С изменением температуры плотность веществ изменяется. Это происходит из-за ускорения движения атомов. У воды наблюдается особое соотношение этих параметров.

Измерение истинной плотности

Рассматривая плотность материала строительства, нужно учитывать его истинный показатель. То есть когда структура вещества единицы объема не содержит в себе раковин, пустот и посторонних включений. На практике нет абсолютной однородности, когда, например, бетон заливают в форму. Чтобы определить реальную его прочность, которая напрямую зависит от плотности материала, проводят следующие операции:

• Структуру подвергают измельчению до состояния порошка. На этом этапе избавляются от пор.
• Просушивают в при температуре свыше 100 градусов, из пробы удаляют остатки влаги.
• Остужают до комнатной температуры и пропускают через мелкое сито с размером ячейки в 0,20 х 0,20 мм, придавая однородность порошку.
• Полученный образец взвешивают на электронных весах высокой точности. Объем вычисляют в объемомере методом погружения в жидкую структуру и измерения вытесненной жидкости (пикнометрический анализ).

Расчет проводят по формуле:

где m — масса образца в г;

V — величина объема в см 3 .

Часто применимо измерение плотности в кг/м 3 .

Примеры задач с решением

Пример 1

Задание. Получите единицу плотности в системе СИ, используя уравнение Менделеева — Клапейрона для идеального газа.

Решение. Запишем уравнение состояния идеального газа в виде:

\

Разделим его правую и левую части на объем, тогда выражение (1.1) преобразуется к виду:

\

Выразим из (1.2) плотность, имеем:

\

тогда:

\=\left=\frac{Па\cdot \frac{кг}{моль}}{\frac{Дж}{моль\cdot К}\cdot К}=\frac{Па\cdot кг}{Дж}=\frac{Н}{м^2Н\cdot м}\cdot кг=\frac{кг}{м^3}.\]

Ответ. Из уравнения состояния идеального газа получается, что $\frac{кг}{м^3}$ — единицы измерения плотности в системе СИ.

Пример 2

Задание. В замкнутом сосуде заключена смесь из двух газов, азота и углекислого газа. Массы газов равны $m_{N_2}=7\ г$; $m_{{СО}_2}=11\ г$. Температура смеси $T=290\ К$, давление $p={10}^5Па$. Какова плотность смеси ($\rho $), если газы принять за идеальные? Выразите плотность в $\frac{г}{л}.$\textit{}

Решение. Сделаем рисунок.

Плотность смеси найдем как:

\

где $V$ — объем смеси газов. Объем смеси газов найдем, используя уравнение состояния идеального газа:

\

где $\nu ={\nu }_{N_2}+{\nu }_{{СО}_2}=\frac{m_{N_2}}{{\mu }_{N_2}}+\frac{m_{{СО}_2}}{{\mu }_{{СО}_2}}$ — количество вещества смеси$;;\ {\mu }_{N_2}=28\cdot {10}^{-3}\frac{кг}{моль};;\ {\mu }_{{СО}_2}=44\cdot {10}^{-3}\frac{кг}{моль}$ — молярные массы рассматриваемых веществ. Выразим объем из (2.2), имеем:

\

Подставим найденный в (2.3) объем в формулу (2.1), получим:

\

Переведем все единицы в систему СИ, проведем вычисления:

\

Переведем $\frac{кг}{м^3}$ в $\frac{г}{л}$, если известно, что 1 кг=1000 г; 1$м^3$=1000 л, тогда:

\

Ответ. $\rho =1,49\frac{\ г}{л}$

Как найти плотность объекта по массе и объему (шаг за шагом):

Рассчитать плотность с помощью этого расчет плотности очень просто. Вы можете найти любое из трех значений, введя два значения в формулу. Вот пример для каждого расчета:

Проведите по!

Пример:

Объект весил около 150 г и объем 90 см3. Найти плотность объекта?

Решение:

Формула:

р = м / В

Вот,

m = 150 г

V = 90 см3

Так,

р = 150/90

p = 1,66 г · см-3

как определить плотность объем по и массе:

Вы можете легко определить объем объекта, изменив уравнение плотности. Давайте посмотрим на пример:

Пример:

Какой у тела объем, если его масса 500 г, а плотность 4 см-3?

Решение:

Формула:

V = м / п

Вот,

м = 500г

р = 4 см-3

Так,

V = 500/4

V = 125 см3

Как найти массу объекта с учетом плотности и объема:

Расчет массы по объему и плотности становится простым. Просто следуйте следующему примеру:

Пример:

Объем объекта 200 см3, а плотность 9 см-3, какова масса объекта?

Решение:

Формула:

т = р * V

Вот,

V = 200 см3

р = 9 см-3

Так,

т = (9) * (200)

м = 1800г

Плотности астрономических объектов [ править | править код ]

• Средние плотности небесных тел Солнечной системы см. на врезке.
• Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли

10 −21 ÷10 −20 кг/м³. Плотность межзвёздной среды

10 −23 ÷10 −21 кг/м³.

• Плотность межгалактической среды 2×10 −34 ÷5×10 −34 кг/м³.
• Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
• Плотность белых карликов 10 8 ÷10 12 кг/м³
• Плотность нейтронных звёзд имеет порядок 10 17 ÷10 18 кг/м³.
• Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:

ρ = 3 c 6 32 π M 2 G 3 . ho =<3,c^<6>><32pi M^<2>G^<3>>>.>Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ

M −2 ). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 10 19 кг/м³, превышающей ядерную плотность (2×10 17 кг/м³), то сверхмассивная чёрная дыра с массой в 10 9 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).

Испытания на плотность, дробимость и не только

Адгезия – способность вяжущих веществ сцепляться с щебнем. Фото Грунтовозов

Испытания в полевых и лабораторных условиях позволяет рассчитать не только плотность, но и другие характеристики:

Прочность или дробимость определяется посредством механического воздействия и вычисления процента потери массы после раздавливания.

Морозостойкость определяется двумя способами: 1) метод попеременного замораживания и оттаивания и 2) ускоренный метод.

Истираемость определяется посредством прокручивания материала с металлическими шарами в полочном барабане.

Адгезия. Показатель возможно определить визуально: камни с шероховатой поверхностью имеют лучший показатель по сравнению с гладкими; мытый щебень лучший в сравнении с немытым. Некоторые источники утверждают, что показатель адгезии зависит от цвета камней, однако это мнение ошибочно

Кроме этого, важно знать, что на показатель влияет лещадность, щебень с малым содержанием зерен неправильной формы обладает отличным сцеплением с вяжущими веществами. Точный показатель определяется в лабораторных условиях.

Водостойкость определяется посредством прохождения щебнем циклов насыщения водой и высушивания.

Упражнение 7

1. Плотность редкого металла осмия равна 22 600 кг/м 3 . Что это означает? 2. Пользуясь таблицами плотностей (табл. 2, 3), определите, плотность какого вещества больше: цинка или серебра; бетона или мрамора; бензина или спирта.

3. Три кубика — из мрамора, льда и латуни — имеют одинаковый объём. Какой из них имеет большую массу, а какой — меньшую? 4. Самое лёгкое дерево — бальза. Масса древесины этого дерева равна 12 г при объёме 100 см 3 . Определите плотность древесины г/см 3 и кг/м 3 . 5. Кусочек сахара имеет размеры: а = 2,5 см, b = 1 см, с = 0,7 см (рис. 53). Его масса равна 0,32 г. Определите плотность сахара. Проверьте полученный результат по таблице 2.

Плотность воды в зависимости от температуры

Принято считать, что плотность воды равна 1000 кг/м3, 1000 г/л или 1 г/мл, но часто ли мы задумываемся при какой температуре получены эти данные?

Максимальная плотность воды достигается при температуре 3,8…4,2°С. В этих условиях точное значение плотности воды составляет 999,972 кг/м3. Такая температурная зависимость плотности характерна только для воды. Другие распространенные жидкости не имеют максимума плотности на этой кривой — их плотность равномерно снижается по мере роста температуры.

Вода существует как отдельная жидкость в диапазоне температуры от 0 до максимальной 374,12°С — это ее критическая температура, при которой исчезает граница раздела между жидкостью и водяным паром. Значения плотность воды при этих температурах можно узнать в таблице ниже. Данные о плотности воды представлены в размерности кг/м3 и г/мл.

В таблице приведены значения плотности воды в кг/м3 и в г/мл (г/см3), допускается интерполяция данных. Например, плотность воды при температуре 25°С можно определить, как среднее значение от величин ее плотности при 24 и 26°С. Таким образом, при температуре 25°С вода имеет плотность 997,1 кг/м3 или 0,9971 г/мл.

Значения в таблице относятся к пресной или дистиллированной воде. Если рассматривать, например, морскую или соленую воду, то ее плотность будет выше — плотность морской воды равна 1030 кг/м3. Плотность соленой воды и водных растворов солей можно узнать в этой таблице. Плотность воды при различных температурах — таблица

t, °С	ρ, кг/м3	ρ, г/мл	t, °С	ρ, кг/м3	ρ, г/мл	t, °С	ρ, кг/м3	ρ, г/мл
999,8	0,9998	62	982,1	0,9821	200	864,7	0,8647
0,1	999,8	0,9998	64	981,1	0,9811	210	852,8	0,8528
2	999,9	0,9999	66	980	0,98	220	840,3	0,8403
4	1000	1	68	978,9	0,9789	230	827,3	0,8273
6	999,9	0,9999	70	977,8	0,9778	240	813,6	0,8136
8	999,9	0,9999	72	976,6	0,9766	250	799,2	0,7992
10	999,7	0,9997	74	975,4	0,9754	260	783,9	0,7839
12	999,5	0,9995	76	974,2	0,9742	270	767,8	0,7678
14	999,2	0,9992	78	973	0,973	280	750,5	0,7505
16	999	0,999	80	971,8	0,9718	290	732,1	0,7321
18	998,6	0,9986	82	970,5	0,9705	300	712,2	0,7122
20	998,2	0,9982	84	969,3	0,9693	305	701,7	0,7017
22	997,8	0,9978	86	967,8	0,9678	310	690,6	0,6906
24	997,3	0,9973	88	966,6	0,9666	315	679,1	0,6791
26	996,8	0,9968	90	965,3	0,9653	320	666,9	0,6669
28	996,2	0,9962	92	963,9	0,9639	325	654,1	0,6541
30	995,7	0,9957	94	962,6	0,9626	330	640,5	0,6405
32	995	0,995	96	961,2	0,9612	335	625,9	0,6259
34	994,4	0,9944	98	959,8	0,9598	340	610,1	0,6101
36	993,7	0,9937	100	958,4	0,9584	345	593,2	0,5932
38	993	0,993	105	954,5	0,9545	350	574,5	0,5745
40	992,2	0,9922	110	950,7	0,9507	355	553,3	0,5533
42	991,4	0,9914	115	946,8	0,9468	360	528,3	0,5283
44	990,6	0,9906	120	942,9	0,9429	362	516,6	0,5166
46	989,8	0,9898	125	938,8	0,9388	364	503,5	0,5035
48	988,9	0,9889	130	934,6	0,9346	366	488,5	0,4885
50	988	0,988	140	925,8	0,9258	368	470,6	0,4706
52	987,1	0,9871	150	916,8	0,9168	370	448,4	0,4484
54	986,2	0,9862	160	907,3	0,9073	371	435,2	0,4352
56	985,2	0,9852	170	897,3	0,8973	372	418,1	0,4181
58	984,2	0,9842	180	886,9	0,8869	373	396,2	0,3962
60	983,2	0,9832	190	876	0,876	374,12	317,8	0,3178

Следует отметить, что при увеличении температуры воды (выше 4°С) ее плотность уменьшается. Например, по данным таблицы, плотность воды при температуре 20°С равна 998,2 кг/м3, а при ее нагревании до 90°С, величина плотности снижается до значения 965,3 кг/м3. Удельная масса воды при нормальных условиях значительно отличается от ее плотности при высоких температурах. Средняя плотность воды, находящейся при температуре 200…370°С намного меньше ее плотности в обычном температурном диапазоне от 0 до 100°С.

Смена агрегатного состояния воды приводит к существенному изменению ее плотности. Так, величина плотности льда при 0°С имеет значение 916…920 кг/м3, а плотность водяного пара составляет величину в сотые доли килограмма на кубический метр. Следует отметить, что значение плотности воды почти в 1000 раз больше плотности воздуха при нормальных условиях.

Кроме того, вы также можете ознакомиться с таблицей плотности веществ и материалов.

Определение плотности жидкости ареометром

Плотность жидкости может быть приближенно (с точностью до 0,01) определена с помощью ареометра. Этот метод находит широкое практическое применение при определении относительной плотности серной, азотной и соляной кислот, этилового спирта и др. Достоинствами этого метода являются быстрота определения и возможность использования для анализа вязких жидкостей. К недостаткам метода, помимо невысокой точности, следует отнести необходимость использования относительно большого количества анализируемой жидкости.

Ареометр (рис. 5) представляет собой стеклянный тонкостенный цилиндрический сосуд, расширяющийся внизу и имеющий на конце стеклянный резервуар, заполненный дробью, реже ртутью. В верхней части ареометра имеется шкала с делениями, соответствующими относительной плотности жидкости, и указанием температуры, при которой следует производить определение. Имеются ареометры для жидкостей легче и тяжелее воды, для серной кислоты, едких щелочей, а также ряд специальных ареометров для измерения плотности спирта (спиртометр), молока (лактометр) и др. Для повышения точности измерения промышленность выпускает наборы ареометров, шкалы которых охватывают определенный диапазон плотностей.

Рис. 5. Ареометр.

Как правило, градуировку ареометров производят при 20 С и относят к плотности воды при 4 С, поэтому показания шкалы дают величину d. Если в соответствии с указаниями стандарта температура анализируемой жидкости отличается от температуры, указанной на шкале ареометра, то следует внести поправку на разницу температур.

Испытуемую жидкость помещают в цилиндр емкостью не менее 0,5 л и при температуре жидкости 20 С осторожно опускают в нее чистый сухой ареометр. Погружать ареометр в жидкость следует осторожно, не выпуская его из рук до тех пор, пока не станет очевидным, что он плавает

При этом ареометр должен находиться в центре цилиндра и ни в коем случае не касаться стенок и дна сосуда. Отсчет производят по делениям шкалы ареометра через 3-4 мин после погружения по нижнему мениску жидкости. В случае определения плотности темноокрашенных жидкостей отсчет производят по верхнему мениску. После определения ареометр моют, вытирают и убирают в специальный футляр.

Как влияют внешние воздействия на расчет

Понятие «плотность» зависимо от условий окружающей среды, в которых происходит ее измерение. По мере повышения либо понижения температуры плотность начинает постепенно уменьшаться. Например, плотность воды при температуре кипения составляет 958,4 кг/м3. Однако таким образом ведут себя не все жидкости. Многие, испытывая понижение температуры, увеличивают свою плотность.

Водка при 20°C имеет плотность 935 кг/м3, а при 80°C — 888; нафталин при 230°C — 865 кг/м3, при 320°C — 794 кг/м3; раствора сахара при 20°C — 1333 кг/м3, при 100°C — 1436 кг/м3. Значение аналогичных величин вынесены в специальные таблицы, которые носят справочный характер.

Для вычисления ρ при изменении температуры вещества применяется формула:

Примеры плотности разных веществ

Вода имеет плотность 1000 кг / м³ (т.е. 1 г / см³). Это не совпадение. Исторически сложилось так, что один литр воды, при четырех градусах Цельсия при нормальном давлении, считался эталоном 1 кг массы.

Железо, платина, золото и свинец — материалы с высокой плотностью. Многие виды горных пород и минералов также являются очень плотными. Чаще всего они отличаются большим весом и твердостью. Противоположность им — это разреженный материал, например, бамбук, алюминий или пенополистирол.

Как правило, жидкости менее плотны, чем твердые тела, а газы — чем жидкости. Это связано с тем, что твердые тела имеют плотно прилегающие частицы, в жидкостях частицы могут скользить друг вокруг друга, а в газах они свободно перемещаются.

Какая плотность у различных твердых материалах, жидкостях и газах, вы узнаете из наших таблиц.

Таблица1. Плотность твердых веществ при стандартной температуре 20 ° C

	кг/м³
графит	2300–2720
гипс	2320
кремний	2330
бериллий	2700
алюминий	2720
кварц	2300–2700
цинк	7131
медь	8960
латунь	8200–8950
платина	21 410
нержавеющая сталь	8100
золото	19 320
тополь	350–400
липа	320–590
сосна	370–600
дубовая древесина	600–900
кованое железо	7800–7900
лед (0 ° C)	920
каменная соль	2160

Таблица 2. Плотность жидкостей

	кг/м³
этанол	791
жидкий азот (–196 ° C)	808
бензин	700
эфир	720
глицерин	1260
масло	800
ртуть	13 550
дистиллированная вода (4 ° C)	1000
жидкий водород (–253 ° C)	71

Таблица 3. Плотность газов при стандартном атмосферном давлении 101325 Па

Газы	кг/м³
аргон	1,784
азот	1,250
хлор	3,22
углекислый газ	1,98
этан	1,36
гелий	0,178
метан	0,717
воздух	1,293
кислород	1,429
водород	0,09

Простое объяснение физического понятия о плотности веществ вы найдете в нашем видео.

Читайте далее:

Онлайн конвертер объема, единицы и системы измерения, конвертация величин объема

Онлайн конвертер площади, единицы измерения площади в разных системах, их быстрый перевод

Онлайн конвертер длины, перевод всех систем измерения, метрическая, британо-американская, старорусская, морская, астрономическая, типографская

Онлайн конвертер долей, перевод дюжин, процентов, промилле и других единиц

Конвертер температур, перевод градусов Цельсия, Фаренгейта, Кельвина, Реомюра

Расход затирки для плитки на 1 м² — калькулятор, формула расчета

Примеры решения задач

Задание. Какова плотность воды, если объем, который занимает одна молекула H₂O, примерно равен $Delta V approx 3 cdot 10^$ м 3 ? Считайте, что молекулы в воде плотно упакованы.

Решение. Если считать, что молекулы в воде плотно упакованы, то ее плотность можно найти как:

где m – масса молекулы воды. Найдем m, используя известное соотношение:

где N=1 — количество молекул (в нашем случае одна молекула), m — масса рассматриваемого количества молекул (в нашем случае m=m), N_А=6,02• 10 23 моль -1 – постоянная Авогадро, $mu$=18•10 -3 кг/моль (так как относительная молекулярная масса воды равна M_r=18). Следовательно, применяя выражение (2) для нахождения массы одной молекулы имеем:

Подставим m в выражение (1), получаем:

Проведем расчет искомой величины:

Ответ. Плотность воды равна 10 3 кг/м 3 .

Формула плотности вещества не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Какова плотность кристаллов хлорида цезия (CsCl), если кристаллы имеют кубическую кристаллическую решетку (рис.1) в вершинах которой находятся ионы хлора (Cl — ), а в центре расположен ион цезия (Cs + ). Ребро кристаллической решетки считайте равным d=0, 41 нм.

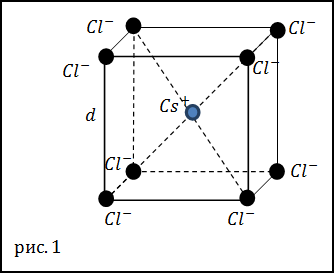
Решение. За основу решения задачи примем выражение:

В выражении (2.2) массу молекулы можно выразить через ее плотность как:

где V_m – объем исследуемой молекулы. Так как кристаллы имеют кубическую кристаллическую решетку, ребро которой нам известно (и равно d), то вместо объема V_m можно использовать выражение:

Подставим выражения (2.3) и (2.4) в формулу (2.2), получим:

Тогда выражение для плотности примет вид:

Переведем размер стороны кристаллической решетки в единицы системы СИ, получим d=0,41нм=0, 41•10 -9 ) м. Проведем вычисления:

Ответ. $rho=4047,6$ кг/м 3

Вязкость жидкостных веществ

Вторым обязательным параметром каждого жидкостного вещества считается вязкость. Данное состояние жидкостного вещества способно производить противодействие любой наружной силе. Все существующие жидкостные вещества оснащены данным свойством. Вязкость формируется как внутреннее трение при сравнительном смещении частиц жидкостного вещества, которые находятся рядом. В реальности имеются как легко движущиеся жидкостные вещества, так и вещества с большой вязкость.

В первую категорию входят воздух и вода. В тяжёлых масляных веществах противодействие осуществляется на другом уровне. Вязкость возможно квалифицировать уровнем текучести жидкостного вещества. Данное явление именуют подвижностью частиц данного вещества, и этот процесс находится в полной зависимости от плотности жидкости. Вязкость жидкостных веществ в условиях лаборатории устанавливают с помощью вискозиметра. Когда вязкость жидкостного вещества находится в большой зависимости исключительно от температурных параметров, тогда различаются некоторое количество главных характеристик жидкости.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Решение задач Контрольные работы Эссе

Увеличивая температурные параметры капельной жидкостного вещества, вязкость стремительно уменьшается. Вязкость газообразной жидкости при данных действиях исключительно растёт. Сила наружного трения в жидкостных веществах создаётся при соответствии скорости градиента к площади пластов, осуществляющих трение. В то же время трение в жидкостных веществах различается от явлений трения в других объектах, в частности, в объектах твёрдого вида. В твёрдых объектах сила трения зависима от стабильного давления, а не от участка поверхностей, которые трутся.

Примеры решения задач

Задача 1

Условие: имеется алюминиевый брусок со сторонами 3, 5 и 7 сантиметров. Какова его масса?

Решение:

Найдем объем бруска:

V = a * b * c;

V = 3 * 5 * 7 = 105 см3;

Табличное значение плотности алюминия: 2800 кг/м3 или 2,8 г/см3;

Вычислим массу бруска:

m = V * ρ;

m = 105 * 2,8 = 294 г.

Ответ: m = 294 г. 

Задача 2 

Задача по смежной теме.

Условие: сколько энергии потребуется для того, чтобы довести воду комнатной температуры (20 градусов Цельсия) из стакана (ёмкость 200 мл) до температуры кипения?

Решение:

Найдем недостающую информацию: температура кипения воды t₂ = 100 градусов Цельсия, удельная теплоемкость воды с = 4200 Дж/кг * С, плотность воды 1 г/см3, 1 мл воды = 1 см3;

Найдем массу воды:

m = V * ρ;

m = 200 * 1 = 200 г = 0,2 кг;

Найдем энергию:

Q = c * m * (t₂ – t₁);

Q = 4200 * 0,2 * (100 – 20) = 67200 Дж = 67,2 кДж.

Ответ: Q = 67,2 кДж.

Задача 3

Задача с молярной массой.

Условие: найдите массу CO₂ при объеме в 5,6 л.

Решение:

Найдем молярную массу CO₂ :

M = 12 + 16 * 2 = 44 г/моль;

Найдем количество вещества через объем:

n = 5,6 / 22,4 = 0,25 моль;

Найдем массу:

m = n * M;

m = 0,25 * 44 = 11 г.

Ответ: m = 11 г.

Молярная масса элементов и соединений

Соединения — вещества, состоящие из различных атомов, которые химически связаны друг с другом. Например, приведенные ниже вещества, которые можно найти на кухне у любой хозяйки, являются химическими соединениями:

• соль (хлорид натрия) NaCl
• сахар (сахароза) C₁₂H₂₂O₁₁
• уксус (раствор уксусной кислоты) CH₃COOH

Молярная масса химических элементов в граммах на моль численно совпадает с массой атомов элемента, выраженных в атомных единицах массы (или дальтонах). Молярная масса соединений равна сумме молярных масс элементов, из которых состоит соединение, с учетом количества атомов в соединении. Например, молярная масса воды (H₂O) приблизительно равна 1 × 2 + 16 = 18 г/моль.

Что влияет на этот параметр?

В обычных условиях на параметры воды значительное влияние оказывает степень нагрева. Как правило, у большинства веществ или соединений плотность увеличивается при понижении температуры. Однако, у воды эта зависимость нелинейная.

Показатель достигает максимума при 4°C, понемногу уменьшаясь как при понижении, так и при повышении температуры. При этом, когда вода переходит в твердую фазу (образуется лед), процесс уменьшения плотности при охлаждении продолжается.

Этим объясняется известный (и очень опасный для оборудования) эффект расширения воды при замерзании — из 0,028 м3 воды получается 0,03 м3 льда.

Зависимость физических свойств от температуры наблюдается практически у всех веществ, но только вода демонстрирует это в жидком состоянии.

При этом горячая вода показывает нелинейный, но относительно ровный график уменьшения значений (по крайней мере, до точки кипения в 100°С).

Пример

Допустим, машина привезла щебень на строительную площадку. Как провести необходимые измерения? Для этого подсчитывается объем груза и кузова по границе заполнения. Затем полученные значения умножаются на коэффициент уплотнения. Понятно, что цифры будут разными за счет «утряски» груза во время движения, но он не может потерять в массе. В первом случае, с учетом усадки, можно сказать, что это общая плотность щебня или значение, близкое к ней. Во втором – насыпная.

Для лучшего понимания возьмем другой жизненный пример. Купили некоторое количество сахара. Скажем, килограмм. Засыпали в сахарницу, получили первичный объем. Потрясли, постучали, утрамбовали. Измерили. Получили в результате конечный объем.

Совет

Следует помнить о том, что насыпная плотность – это качество натуральное, природное, исключающее возможность последующей трамбовки для устранения пустот.

У строительных материалов она является одним из базовых параметров. От этого зависит прочность конечного изделия и косвенное определение пустот, заполненных менее прочным составом из других элементов.

При изготовлении бетонных смесей руководствуются правилом: чем выше значение фракции, тем ниже параметры насыпной плотности. Знание ее показателей позволяет существенно сэкономить. Например, при низком значении фракции и высокой насыпной плотности цемента потребуется на порядок меньше. Со знанием точных объемов упрощается транспортировка и хранение. Становится возможным подсчитать материал для перевозки. Также в данном случае можно учесть грузоподъемность транспорта.